So, this is my first post in a while. I changed jobs in January, and moved back across the country to my hometown of Boise, ID. I was hoping that my first post-move update would be more uplifting, but by mid-March, I didn’t want to write anything, for a variety of reasons. As a person whose job involves cleaning and analyzing data, the pandemic has been surreal– public health, statistical methods, and data visualizations are now daily topics, for basically everyone I talk to. Early on, I decided that I would not attempt to work with the deluge of public data that was being made available. I like exploring datasets as a hobby, but I didn’t want to add to the noise, and I didn’t want to mislead friends/family that might look at something I’d post.
However, it seems this hasn’t stopped other folks from engaging in some amateur modeling.1 One of my parents forwarded me some graphics that an acquaintance was creating with data from their state. They were plotting cumulative counts over time, and using a linear model to summarize the trend. In the email chain, responding to a discussion about how cautious their community ought to be, they used their results to suggest that their state’s trend was “statistically flat”. The implication seemed to be that the situation was stable, or unlikely to get worse. They weren’t providing projections with the figures themselves, but this posture is still predictive, and leverages the model as supportive evidence. Linear models can sometimes be helpful to (roughly) describe rates of change, but I’m going use my state’s trajectory to show why this reasoning isn’t great.
Let’s pretend we’re back in mid-May, and I start watching my state’s data.2 Using the cumulative counts, I fit a model from 4/15/20 to 5/15/20. I have a big \(R^2\) value (0.996), and the model estimates around 26 new cases each day.3 Great. In black, I’ve plotted the actual cumulative count of cases. The blue line is what the model estimates (the line of best fit), with predictions shown through to 5/30/20.
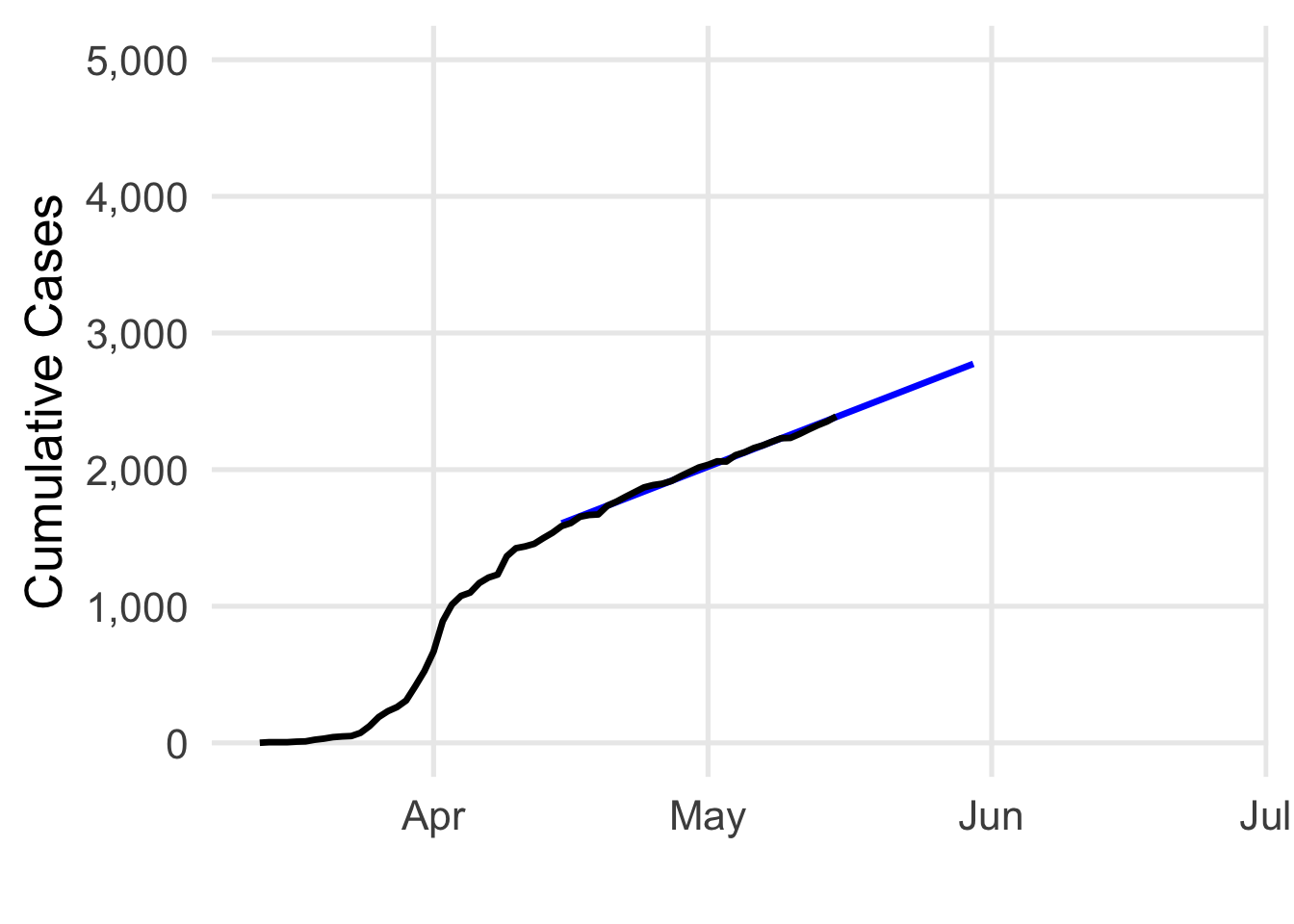
Going along, we see more data. Let’s check back at the end of the month. The progress is measured with the dotted points– the model’s predictions look pretty good!
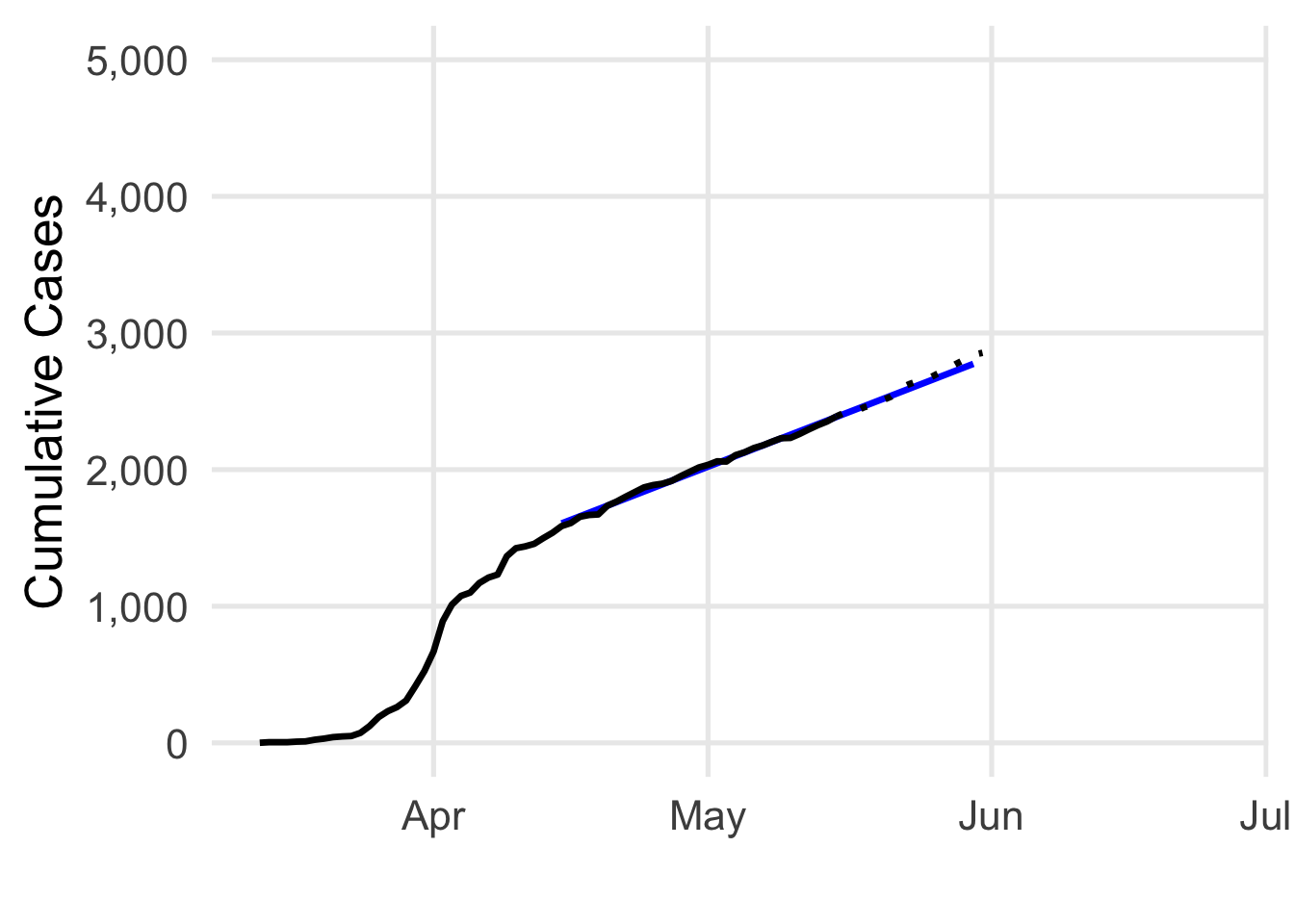
Maybe now I decide to update the model. I’ve redrawn the blue line with data from 4/15/20 to 5/30/20, and we’ll project into June. I still have a big \(R^2\) value (0.997), and the model now estimates 27 new cases each day. Cool.
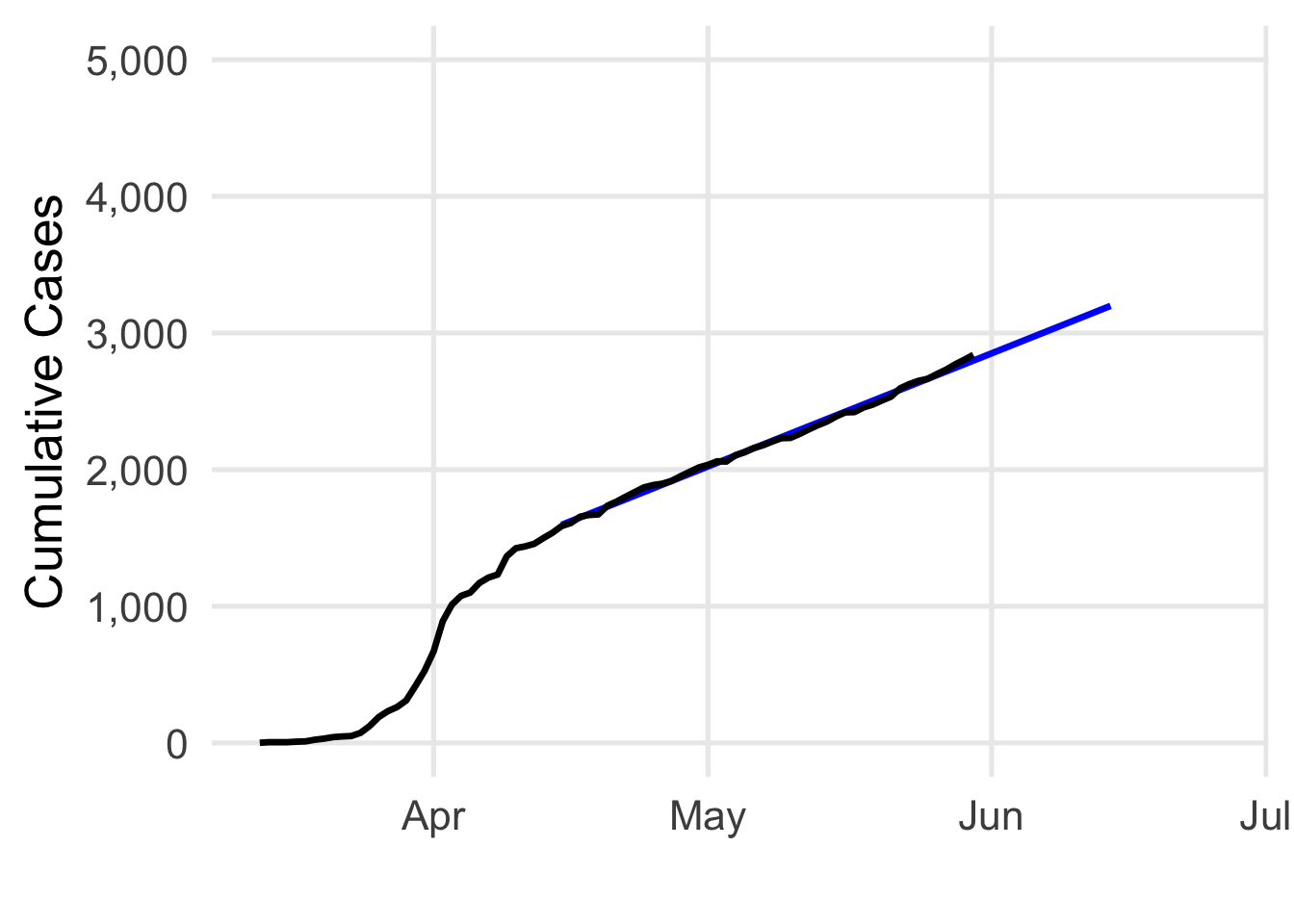
Now I sit back for another few weeks, and check back in the middle of June. Hold on, something seems to be happening…
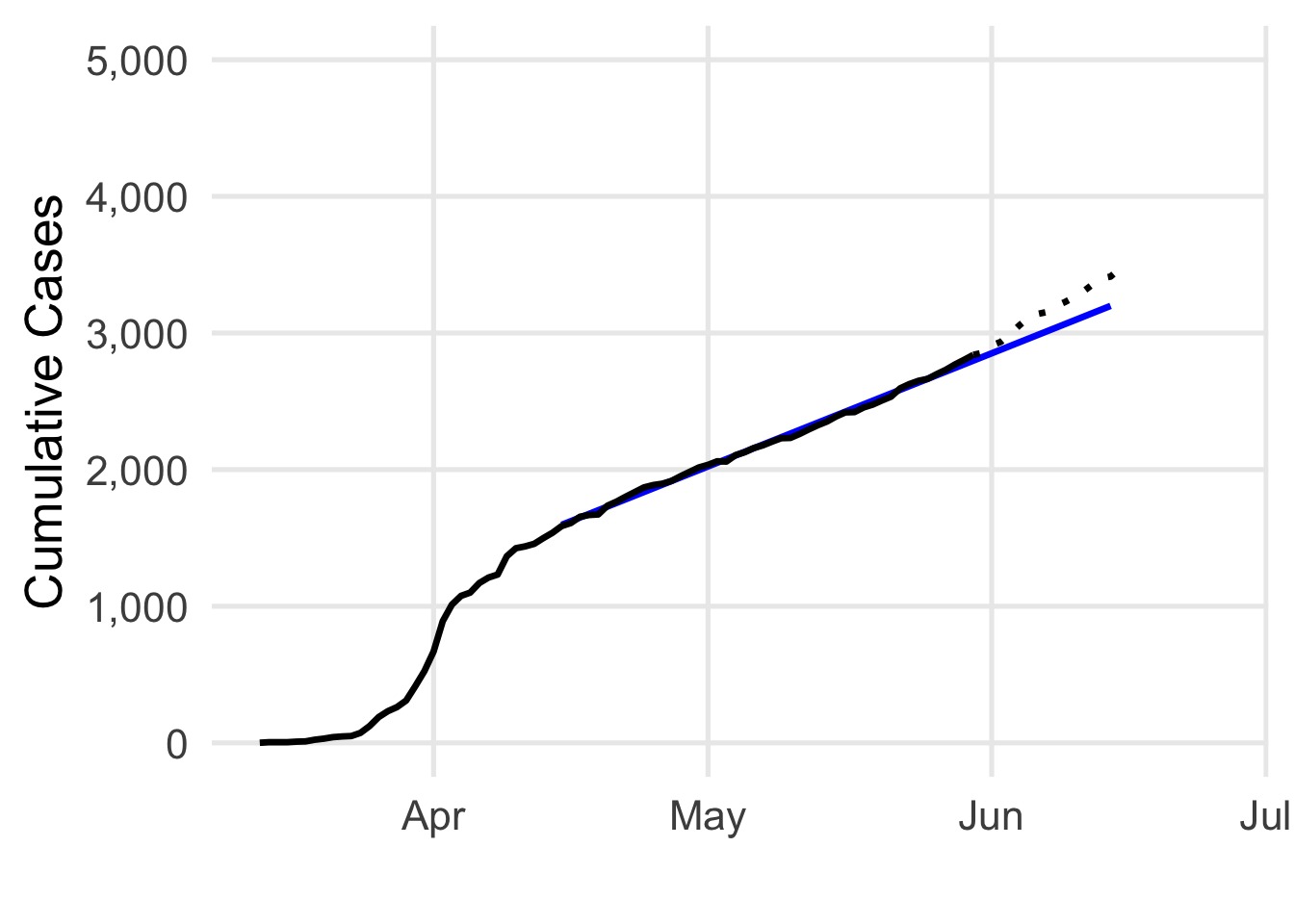
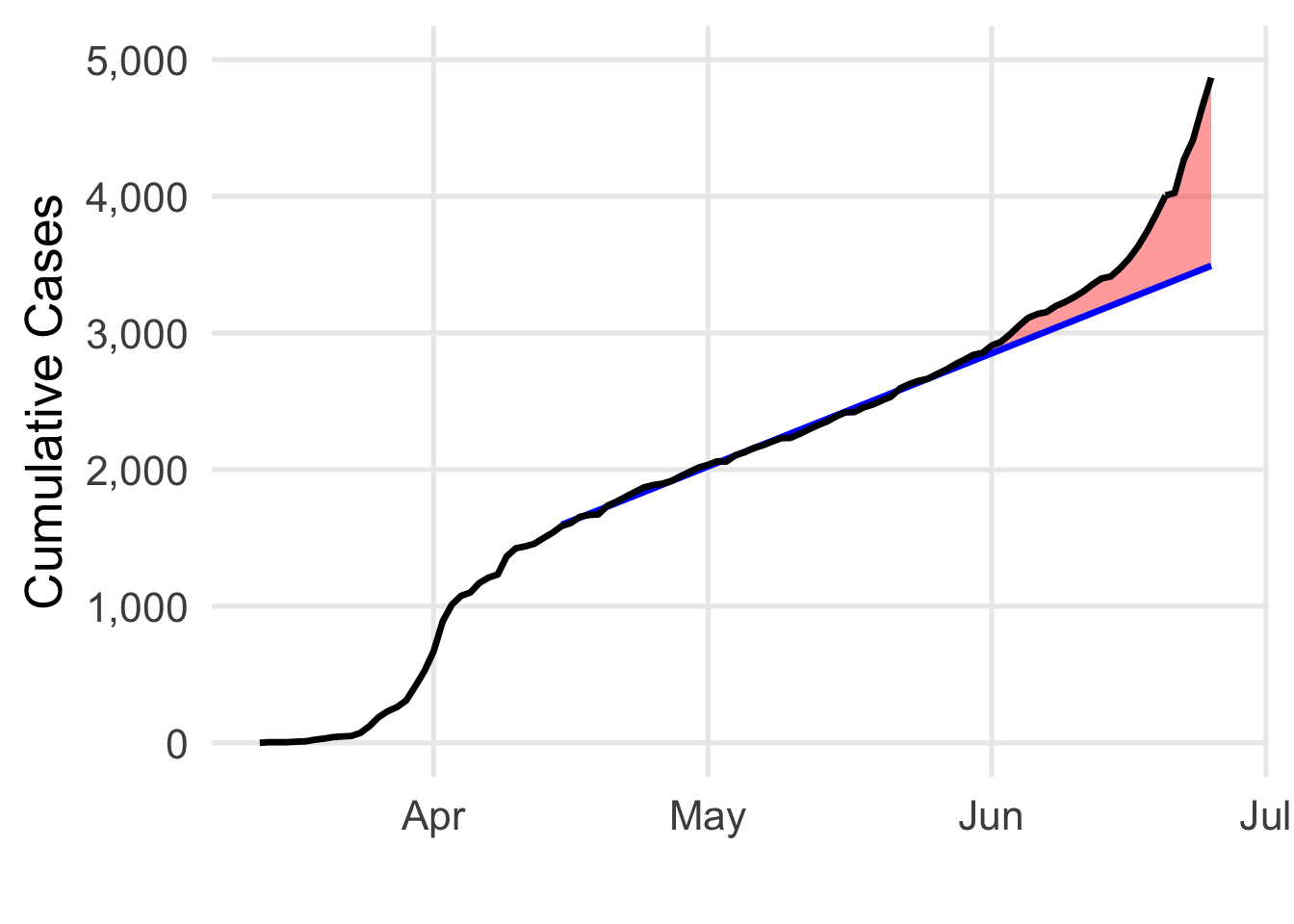
Well, here we are today, and yikes! My predictions for June aren’t looking so good. The number of cases has really started to climb! So, what’s going on here? Conditions appear to have changed, but our model would assume that we’d still be under 4,000 cases at this point. In red, I’ve shaded the difference between the actual case count and what our model would predict. The distances between observed data and predictions is called error. Now we’re able to talk about one of the fundamental limitations in the model we’ve been using: it can’t be used to predict non-linear change.
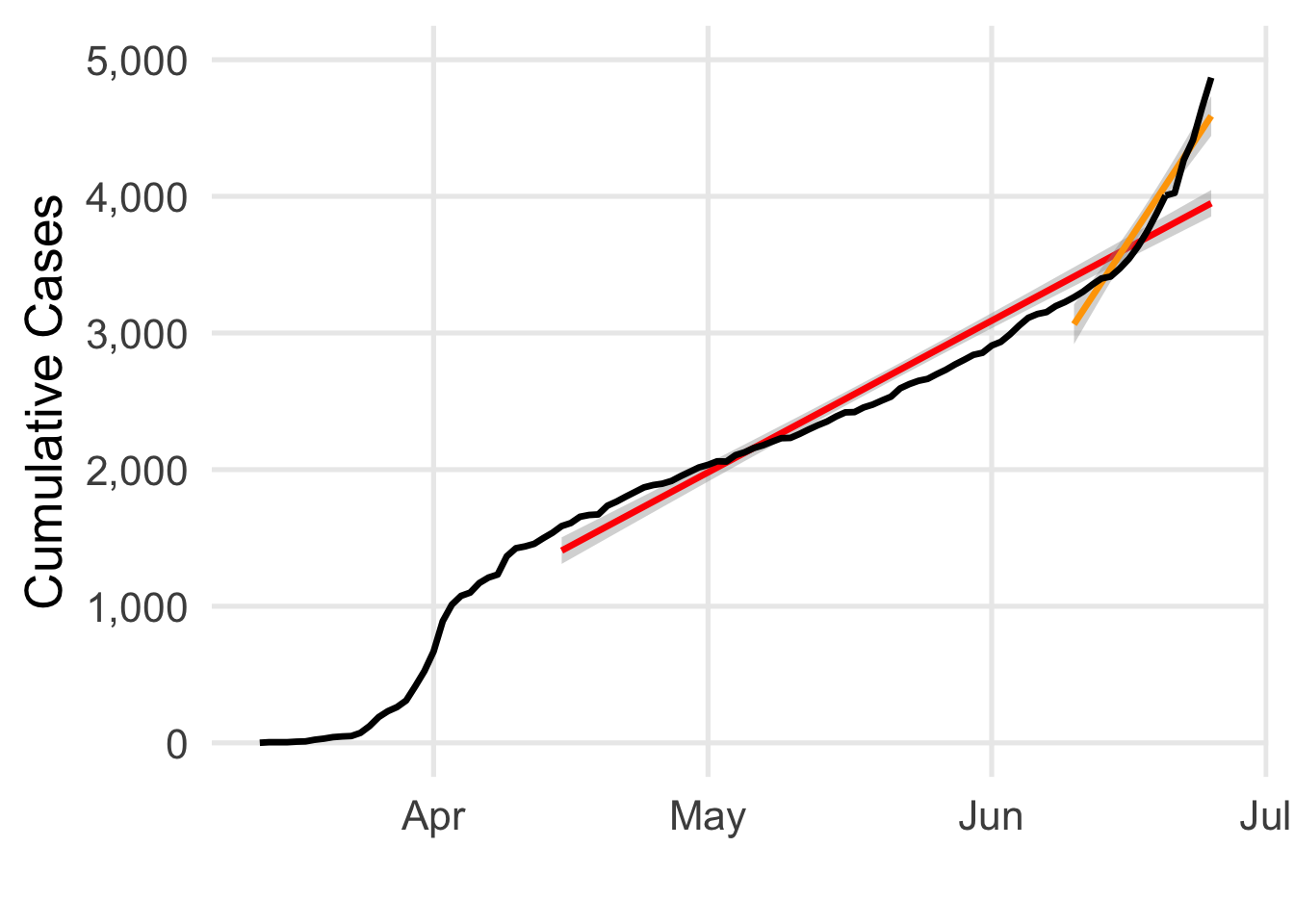
Here’s what linear models built using two different parts of the series look like. First, in red, is what the model would look like if I used all the data I had from 4/15/20 until today. Next, in orange, is what the model looks like using data from 6/10/20 to 6/26/20. The differences are huge! It’s clear how the full model (red) starts to severely mismatch what’s happening; we go from a slope of 37 to ~111 cases per day! While you can barely see it, the shading around each line is meant to reflect the model’s uncertainty. But it’s clear that the error estimated by the model doesn’t match the dynamics of the data! When I predict a new day using linear models like these, I’m bound to use my estimated slope to make that calculation. Similarly, the confidence or uncertainty I have in my prediction is also based on the assumption that errors will be concentrated around the line I’m estimating (with more/less confidence depending on how much data I’ve built the model with).
In short, a trend is only “flat” until it’s not, and a linear model doesn’t help you understand or anticipate such changes, especially when you’re looking at a contagious disease. Perhaps we’re just unlucky, and in another universe, Idaho’s case counts would’ve plateaued until the virus died out. But, this isn’t close to being a reasonable scenario. Yes, the daily increase in new infections was apparently flat, for almost two months. And yes, the models were pretty dang good at summarizing that rate of ~26 new cases per day.4 But this is the wrong curve– we need to flatten the case count of people who have the disease, and the rate at which new cases are created! Because this never happened, it isn’t hard to guess how policy decisions being made by states will interact with these conditions. Idaho permitted bars to open on 5/30/20 and cases spiked roughly 2 weeks later, well in line with what we know about COVID-19’s incubation period. Epidemiological theory and current medical data would predict this, but a naive model (like the ones presented here) can’t.5
- I say “amateur” with humility– for lots of things I’ve tinkered with, I would count myself as such. [return]
- I’m using the NYT’s data: https://github.com/nytimes/covid-19-data [return]
- Obligatory note that a large R^2 value doesn’t mean the model is “good”, see e.g.: https://data.library.virginia.edu/is-r-squared-useless/ [return]
- It’s also worth noting that our level of testing over this period basically guarantees we weren’t detecting all the cases in the community. [return]
- This isn’t to say there aren’t useful approaches to model curves like these! There are plenty of excellent examples attempting to do exactly that for our country and the entire world– stopping with a linear regression isn’t up to the task at hand! [return]