While I don’t think I’ve previously posted about it here, I’ve been a long-time player of the trading card game Magic: the Gathering, primarily enjoying the “limited” format. I keep up with developments in the game largely via Twitter. Last week, an interesting card from the upcoming set, Adventures in the Forgotten Realms (AFR) was previewed.

Lots of potential variation! For those unfamiliar, cards have a “mana value” to reflect their cost to play, usually ranging from 0 to 8. This card’s mana value for example is 3; the two droplet symbols in the top-right corner each count as 1. Tasha’s Hideous Laughter (THL) uses this attribute to exile cards from a player’s deck. You’d put this in a deck where you’d want to make your opponent(s) run out of cards (if a player has to draw from an empty deck, they lose!).
So, how good is it in a limited format, where most decks should contain 40 cards? This card has a higher rarity which means that in a limited deck, you’re unlikely to get multiple copies. You’ll probably only get to cast it once; ideally, it should seal your opponent’s fate of running out of cards. I came across a tweet from @ajlvi, who had set up a quick simulation using an archetypal limited deck to examine this question.1
To give me some idea what Hideous Laughter looks like in limited, I made a sample limited deck with 17 0s, two 1s, six 2s, seven 3s, five 4s, two 5s, and a 6, and then shuffled it and counted CMCs until I reached twenty. After 100,000 iterations: pic.twitter.com/ePO4k2nDgU
— ajlvi (@ajlvi) June 11, 2021
As far as a standard curve in a limited deck, this looks reasonable to me. You can expect to exile 10-13 cards, which is something like 40% of your opponent’s deck if you get to cast THL on turn 3.2
thought experiment: what if THL was in the Strixhaven format?
Going beyond a fixed curve seemed interesting and I wondered what the results would look like with real decklists. We don’t have the full set of cards from the upcoming set, so we can’t speculate on what decks from the future format will look like. However, we could imagine inserting THL into the most recent limited format, Strixhaven. We’re fortunate enough that 17lands.com provides game data, from which we can pull the cards that were listed in a player’s deck. Here I’ll be using games from the Premier Draft queues, gathered between 4/15/21 and 5/12/21. As a note on the format, it’s possible to build decks that can decide a game in the first 4-5 turns (e.g. decks built with cards from the Silverquill college). These “aggro” builds include more cards with lower mana values, which would push the expected number of hits from THL up. But, based on my experience with the format, I would say that the deck archetypes are generally diverse in strategies.3
prepping the 17lands data
I’m very grateful that the folks at 17lands are generously sharing the data, but they require a bit of transformation before use. For the games file, its structure is essentially a wide matrix, with columns dedicated to where a card was seen (e.g., Opening Hand, Deck, Sideboard, etc.). For my purposes, I need to get counts for the number of copies of each card that a player included in their deck. I also need to merge a CMC (mana value) onto each card. The latter step is much easier when each individual card is represented as a row, i.e. storing the data in a tidy form.
I previously deduplicated the games data to get unique decks, but didn’t reshape it. Here I’ll import it, and define a function that will do the transposing.
library(tidyverse)
decks <- vroom::vroom("../../static/data/tashas-hideous-laughter/deck_data_public_17lands_stx_premierdraft.csv.gz")
# from the decks file, take a sample of size N games
# then, go from a wide matrix to a "tall" file of cards
# we'll keep cards where at least 1 copy was seen in the deck
# then, we'll purposefully duplicate rows based on the # of copies recorded
sample_decks <- function(decks, n = 1) {
decks %>%
slice_sample(n = n) %>%
mutate(game_id = 1:n()) %>%
pivot_longer(contains("deck_")) %>%
filter(value > 0) %>%
transmute(
draft_id, game_id,
name = str_remove(name, "deck_"), # to enable merging w/ scryfall data
copies = value
) %>%
uncount(copies)
}In total, we have 101,704 unique decks. Next we’ll get mana values for each card from Scryfall’s API. Here I’m using a package I’m developing that makes working with Scryfall data easier in R. It’s not quite finished, but should be functional for my purposes here.
# keep both the standard set, as well as the Mystical Archive cards from STX
stx_cards <- scRyfall::search_cards(q = "set:sta or (set:stx is:booster)")assumptions & analysis
Okay, now that everything’s mostly in place, we can proceed with the analysis. My hope is to enrich @ajlvi’s findings by accounting for natural variability in the “curves” of mana values found in a given deck. For example, here are 8 histograms for random decks pulled from the dataset. All of these decks except one include 17 lands (which have a mana value of 0), but show some meaningful variation otherwise. For example, THL would seem optimal against Decks #2 and #5.
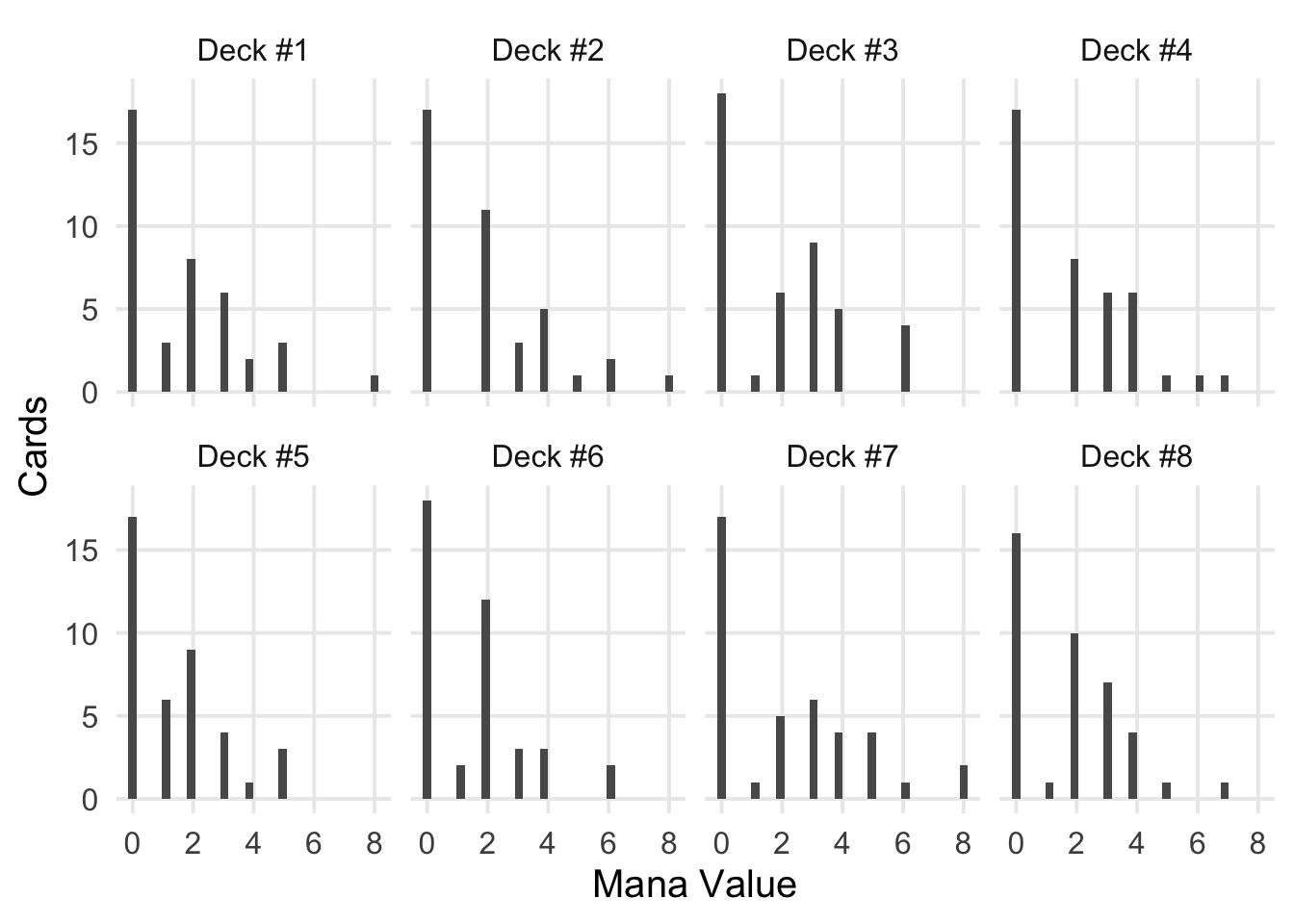
Now we’ll pull the full sample of decks, and perform our experiment. Let’s state the assumptions that we’ll apply to the 101,704 decks:
We’ll assume the player casting THL chose to go first (player 1). This means that the defending player (player 2) will have drawn 1 additional card on their first turn.
Player 2 doesn’t mulligan4 their opening hand.
Player 1 casts THL on turn 3.
In the first two turns, Player 2 casts no spells that would let them draw a card.
This means we’ll shuffle each of the decks, exclude the first 9 cards seen (opening hand of 7, plus cards drawn for 2 turns), and then count the number of cards in order drawn until the cumulative mana value exceeds 20.
set.seed(20210620)
deck <- sample_decks(decks, n = nrow(decks))
deck <- stx_cards %>%
transmute(cmc, name = str_remove(name, " //.*$")) %>% # 17lands drops DFC card names
right_join(deck, by = "name")
thl_hits <- deck %>%
group_by(draft_id, game_id) %>%
slice(sample(1:n())) %>%
slice(9:n()) %>%
mutate(is_20 = cumsum(cumsum(cmc) >= 20)) %>%
filter(is_20 <= 1) %>%
count(name = "hits")Now we’ll look at the observed distribution. Immediately, you can see that despite the additional assumptions and differences in the curves utilized, the results are substantively the same as what @ajlvi shows initially. Theory (re: limited deck construction) seems to carry the day with evaluating this card.
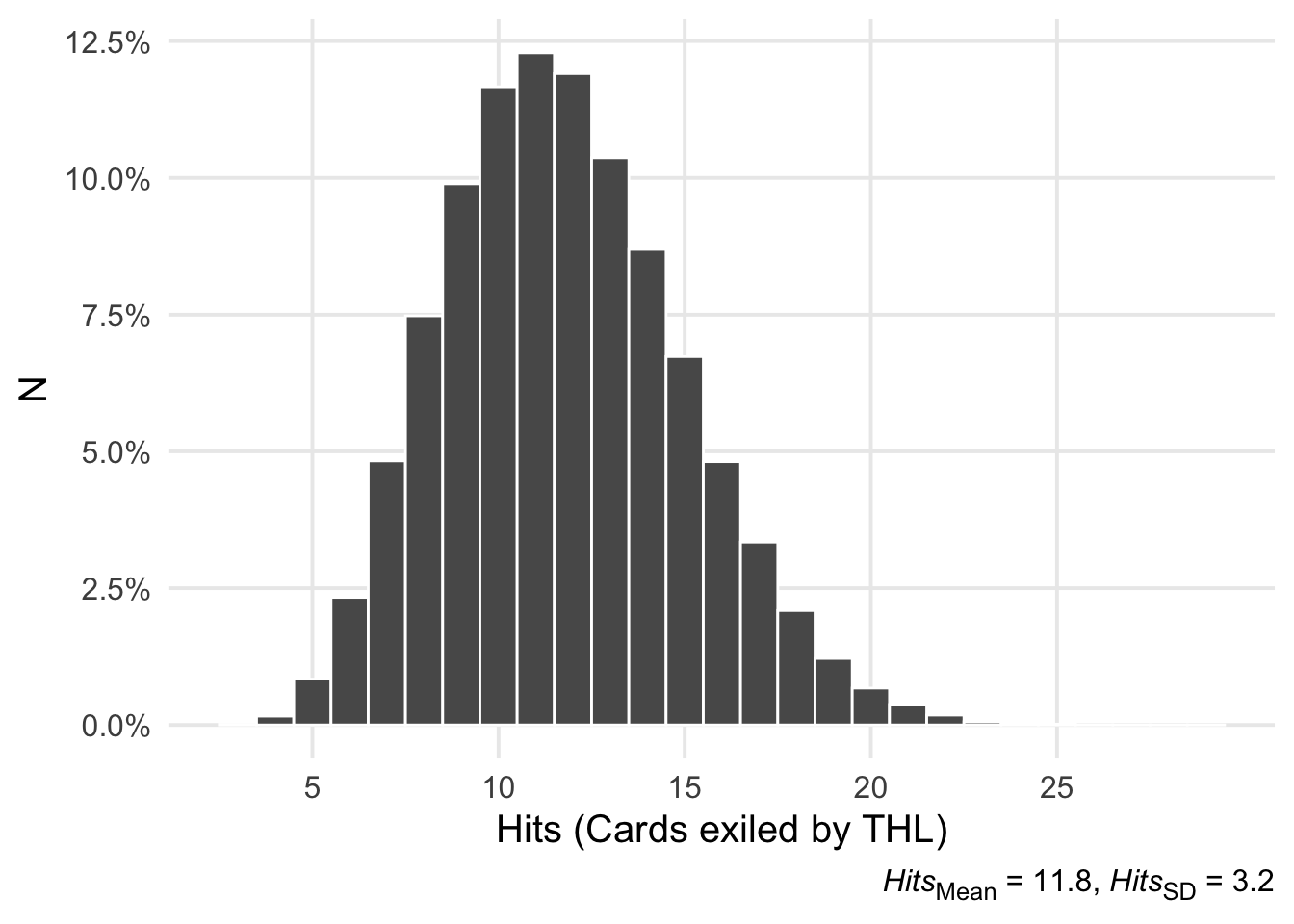
To summarize a bit more, here are some estimated proportions for specific ranges of hits, along with standard errors.
| Estimated Proportions for Specific Ranges | ||
|---|---|---|
| Proportion | SE | |
| Hits < 10 | 0.255 | 0.0014 |
| 10 <= Hits <= 15 | 0.617 | 0.0015 |
| Hits > 15 | 0.128 | 0.0010 |
limitations & conclusions
Assuming the STX format is comparable to AFR, this card seems comparable to Maddening Cacophany (from a recent standard set). If there’s support for mill in the upcoming Adventures in the Forgotten Realms set, this could be worth building around, but it’s not likely to give you free-wins on its own.
For each of the trials, I didn’t check whether the opening hand was worth keeping. This decision is subjective, requiring context and skill, but I could’ve at least ensured that opening hands had >1 and <6 lands.
I’ve sampled games from across the whole range of available days– if there was a significant shift in the 17lands metagame that would have implications for the kinds of mana curves we’d expect to observe, this could have an effect on the results.
Two of the colleges (draft archetypes) in the format encourage building decks with high mana values. Specifically, I’m referring to Quandrix (Blue-Green) and Prismari (Blue-Red). This incentive is more pronounced for Prismari, but I didn’t check the sample to see if this was problematically over-represented. I think this is a marginal consideration, but thought it worth noting.
Wrapping up this post, I wonder how much the results of this analysis depend on THL being cast immediately on turn 3. Phrased differently, is it actually optimal to wait to cast THL until later in the game? I’m inclined to think it’s better to cast THL early, given that most mana curves tend to be centered between 2 and 3. Generally speaking, one is more likely to draw cards with smaller mana-values, which would push down the maximum number of hits you can expect with THL. This is my intuition at least, but maybe I’m missing something!
They’re a good follow if you’re interested in number-crunching re: MtG!↩︎
This is probably not enough to win the game with THL on its own. But it’s powerful, especially if you have other cards that “mill” your opponent, or can guarantee your ability to survive enough time for your opponent to draw the remainder of their deck before you.↩︎
This seems to line up with a quick look at the distribution of turns recorded across the games dataset I’d downloaded. The mean and median # of turns was 10 (with a standard deviation of 3) across 465,319 games.↩︎
This is an action any player can take when looking at their opening hand. If the player would like a different starting hand, they “mulligan” and shuffle their entire deck and re-draw 7 new cards. Once satisfied, they place N many cards on the bottom of their deck, where N is the number of times they took a mulligan.↩︎